Publications
Combining data and theory for derivable scientific discovery with AI-Descartes.
,
2023.
[Nature]
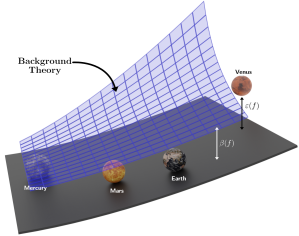
Scientists aim to discover meaningful formulae that accurately describe experimental data. Mathematical models of natural phenomena can be manually created from domain knowledge and fitted to data, or, in contrast, created automatically from large datasets with machine-learning algorithms. The problem of incorporating prior knowledge expressed as constraints on the functional form of a learned model has been studied before, while finding models that are consistent with prior knowledge expressed via general logical axioms is an open problem. We develop a method to enable principled derivations of models of natural phenomena from axiomatic knowledge and experimental data by combining logical reasoning with symbolic regression. We demonstrate these concepts for Kepler’s third law of planetary motion, Einstein’s relativistic time-dilation law, and Langmuir’s theory of adsorption. We show we can discover governing laws from few data points when logical reasoning is used to distinguish between candidate formulae having similar error on the data.
Piecewise-Linear Motion Planning amidst Static, Moving, or Morphing Obstacles.
,
2020.
[Arxiv]
[3min Video]
We propose a novel method for planning shortest length piecewise-linear motions through complex environments punctured with static, moving, or even morphing obstacles. Using a moment optimization approach, we formulate a hierarchy of semidefinite programs that yield increasingly refined lower bounds converging monotonically to the optimal path length. For computational tractability, our global moment optimization approach motivates an iterative motion planner that outperforms competing sampling-based and nonlinear optimization baselines. Our method natively handles continuous time constraints without any need for time discretization, and has the potential to scale better with dimensions compared to popular sampling-based methods.
Semidefinite Representations in Semialgebraic Optimization and Dynamics-Oriented Learning.
,
2020.
PhD Thesis.
[PDF]
[Slides]
Semidefinite programming (SDP) has known a recent surge in popularity in the last few decades in the mathematical optimization community. This surge could be explained by two main reasons. On the one hand, a mature theoretical and computational foundation backing SDP allows one to efficiently compute solutions and obtain formal guarantees on their quality. On the other hand, breakthrough developments connecting SDP to real algebraic geometry have resulted in fundamentally new approaches to tackling semialgebraic optimization problems. The same reasons also make SDP-based approaches well-suited for applications in dynamical systems theory where systems of interest can often be described by algebraic data, and where one seeks to certify various notions of stability, safety, and robustness on the behavior of these systems. The contribution of the first part of this thesis is at the interface of SDP and semialgebraic optimization. We start by presenting a framework for semidefinite programs whose objective function and constraints vary polynomially with time. Our goal is then to find a time-dependent solution that maximizes the aggregate of the objective function over time while satisfying the constraints at all times. We then turn our attention to studying the relationship between two notions that are known to make semialgebraic optimization problems more tractable: the geometric notion of convexity and the algebraic one of being a sum of squares. The interplay between the two notions is poorly understood. For instance, to this date, no example of a convex homogeneous polynomial (of any degree $d$ and in any number of variables $n$) that is not a sum of squares is known. We show that no such example exists in the case where $n=4$ and $d=4$, and if a certain conjecture of Blekherman related to the so-called \emph{Cayley-Bacharach} relationships is true, no such example exists in the case where $n=3$ and $d=6$ neither. These were the two minimal cases where one would have any hope of seeing convex homogeneous polynomials that are not sums of squares, due to known obstructions. %The main ingredient of the proof is a generalization of %the classical Cauchy-Schwarz inequality. In the second part of this thesis, we study the power of SDP and semialgebraic optimization when applied for the task of analyzing dynamical systems. First, we focus on the notion of stability — one of the most fundamental properties that a dynamical system can verify. An ingenious idea, which was proposed by Lyapunov in his thesis at the end of the $19\text{th}$ century, turns the question of testing whether a dynamical system is locally asymptotically stable to the question of existence of an associated \emph{Lyapunov} function; but it was an open question for some time whether this Lyapunov function could be assumed to be a polynomial in the special case where the dynamical system is given by a polynomial vector field with rational coefficients. We give the first example of a globally (and in particular, locally) asymptotically stable polynomial vector field with integer coefficients that does not have an analytic Lyapunov function, let alone a polynomial one. We show by contrast that an asymptotically stable dynamical system given by a {homogeneous} vector field admits a {rational} (i.e., ratio of two polynomials) Lyapunov function, and we give a hierarchy of semidefinite programs that is guaranteed to find this Lyapunov function in finite time. Interestingly, the same tools that help analyze dynamical systems can also be applied for learning these dynamical systems from data. We develop a mathematical formalism of the problem of learning a vector field that fits sample measured trajectories and satisfies a concrete collection of local or global properties (side information). We extend results from constrained polynomial-approximation theory to show that, under some conditions, polynomial vector fields can fit the trajectories of any continuously-differentiable vector field to arbitrary accuracy while respecting side information. Furthermore, we show that SDP-based techniques are particularly suited for this learning task. We end by showing an application to imitation learning problems in robotics.
On sum of squares representation of convex forms and generalized Cauchy-Schwarz inequalities.
,
2019.
SIAM J. Appl. Algebra Geometry, 4(2), 377–400.
[Arxiv]
[Video]
[Sage Notebook]
[Slides]
[SIAM]
A convex form of degree larger than one is always nonnegative since it vanishes together with its gradient at the origin. In 2007, Parrilo asked if convex forms are always sums of squares. A few years later, Blekherman answered the question in the negative by showing through volume arguments that for high enough number of variables, there must be convex forms of degree 4 that are not sums of squares. Remarkably, no examples are known to date. In this talk, we show that all convex forms in 4 variables and of degree 4 are sums of squares. We also show that if a conjecture of Blekherman related to the so-called Cayley-Bacharach relations is true, then the same statement holds for convex forms in 3 variables and of degree 6. These are the two minimal cases where one would have any hope of seeing convex forms that are not sums of squares (due to known obstructions). A main ingredient of the proof is the derivation of certain “generalized Cauchy-Schwarz inequalities” which could be of independent interest.
Teleoperator Imitation with Continuous-time Safety.
,
2019.
RSS 2019.
[Arxiv]
[RSS]
Learning to effectively imitate human teleoperators, with generalization to unseen and dynamic environments, is a promising path to greater autonomy enabling robots to steadily acquire complex skills from supervision. We propose a new motion learning technique rooted in contraction theory and sum-of-squares programming for estimating a control law in the form of a polynomial vector field from a given set of demonstrations. Notably, this vector field is provably optimal for the problem of minimizing imitation loss while providing continuous-time guarantees on the induced imitation behavior. Our method generalizes to new initial and goal poses of the robot and can adapt in real-time to dynamic obstacles during execution, with convergence to teleoperator behavior within a well-defined safety tube. We present an application of our framework for pick-and-place tasks in the presence of moving obstacles on a 7-DOF KUKA IIWA arm. The method compares favorably to other learning-from-demonstration approaches on benchmark handwriting imitation tasks.
Learning Dynamical Systems with Side Information.
,
2019.
SIAM Review, 2023..
[Arxiv]
[SIAM]
[Video]
We present a mathematical and computational framework for the problem of learning a dynamical system from noisy observations of a few trajectories and subject to side information. Side information is any knowledge we might have about the dynamical system we would like to learn besides trajectory data. It is typically inferred from domain-specific knowledge or basic principles of a scientific discipline. We are interested in explicitly integrating side information into the learning process in order to compensate for scarcity of trajectory observations. We identify six types of side information that arise naturally in many applications and lead to convex constraints in the learning problem. First, we show that when our model for the unknown dynamical system is parameterized as a polynomial, one can impose our side information constraints computationally via semidefinite programming. We then demonstrate the added value of side information for learning the dynamics of basic models in physics and cell biology, as well as for learning and controlling the dynamics of a model in epidemiology. Finally, we study how well polynomial dynamical systems can approximate continuously-differentiable ones while satisfying side information (either exactly or approximately). Our overall learning methodology combines ideas from convex optimization, real algebra, dynamical systems, and functional approximation theory, and can potentially lead to new synergies between these areas.
Time-Varying Semidefinite Programs.
,
2018.
Mathematics of Operations Research.
[Arxiv]
We study time-varying semidefinite programs (TV-SDPs), which are semidefinite programs whose data (and solutions) are functions of time. Our focus is on the setting where the data varies polynomially with time. We show that under a strict feasibility assumption, restricting the solutions to also be polynomial functions of time does not change the optimal value of the TV-SDP. Moreover, by using a Positivstellensatz on univariate polynomial matrices, we show that the best polynomial solution of a given degree to a TV-SDP can be found by solving a semidefinite program of tractable size. We also provide a sequence of dual problems which can be cast as SDPs and that give upper bounds on the optimal value of a TV-SDP (in maximization form). We prove that under a boundedness assumption, this sequence of upper bounds converges to the optimal value of the TV-SDP. Under the same assumption, we also show that the optimal value of the TV-SDP is attained. We demonstrate the efficacy of our algorithms on a maximum-flow problem with time-varying edge capacities, a wireless coverage problem with time-varying coverage requirements, and on bi-objective semidefinite optimization where the goal is to approximate the Pareto curve in one shot.
A Globally Asymptotically Stable Polynomial Vector Field with Rational Coefficients and no Local Polynomial Lyapunov Function.
,
2018.
Systems & Control Letters.
[Arxiv]
[ScienceDirect]
We give an explicit example of a two-dimensional polynomial vector field of degree seven that has rational coefficients, is globally asymptotically stable, but does not admit an analytic Lyapunov function even locally.
On Algebraic Proofs of Stability for Homogeneous Vector Fields.
,
2018.
Transactions on Automatic Control.
[Arxiv]
[IEEE]
We prove that if a homogeneous, continuously differentiable vector field is asymptotically stable, then it admits a Lyapunov function which is the ratio of two polynomials (i.e., a rational function). We further show that when the vector field is polynomial, the Lyapunov inequalities on both the rational function and its derivative have sums of squares certificates and hence such a Lyapunov function can always be found by semidefinite programming. This generalizes the classical result that an asymptotically stable linear system admits a quadratic Lyapunov function which satisfies a certain linear matrix inequality. In addition to homogeneous vector fields, the result can be useful for showing local asymptotic stability of non-homogeneous systems, by proving asymptotic stability of their lowest order homogeneous component. We show that in absence of homogeneity, globally asymptotically stable polynomial vector fields may fail to admit a rational Lyapunov function, and that in presence of homogeneity, the degree of the numerator of a rational Lyapunov function may need to be arbitrarily high (even for vector fields of fixed degree and dimension). On the other hand, we also give a family of homogeneous polynomial vector fields that admit a low-degree rational Lyapunov function but necessitate polynomial Lyapunov functions of arbitrarily high degree. This shows the potential benefits of working with rational Lyapunov functions, particularly as the ones whose existence we guarantee have structured denominators and are not more expensive to search for than polynomial ones.